¿Qué es un trío pitagórico?

Un trio o terna pitagórica es una terna (a,b,c) con a, b y c ENTEROS donde
a² + b² = c²

Es decir que cumplen con el teorema de Pitágoras (de ahí el nombre).
Existen infinitos tríos pitagóricos. El más común es (3,4,5), ya que
3² + 4² = 5²


Ejemplos de tríos pitagóricos 


1) (3, 4, 5)
2)(4, 3, 5) 
3)(5, 12, 13) 
4)(6, 8, 10) 
5)(8, 6, 10) 
6)(8, 15, 17) 
7)(9, 12, 15) 
8)(12, 5, 13) 
9)(12, 9, 15)
10)(15, 8, 17)

Demostración de Wiles

El enunciado del último Teorema de Fermat (1601-1665) quedó anotado en un margen de su ejemplar de la Aritmética de Diofanto de Alejandría (150 A.C.) traducida al latín por Claude Gaspar Bachet (1581-1638) publicado en 1621. Este libro, con las numerosas notas marginales de Fermat, fue publicado en 1670 por su hijo Clemente Samuel. El enunciado del teorema dice que la ecuación

no tiene soluciones enteras para n>2. Fermat afirma que tenía una demostración, pero se exime de darla argumentado que el márgen es demasiado estrecho como para dárnosla.

Recientemente, en 1995, Wiles demostró este teorema. Para entender mejor este teorema veamos el caso n=2, para el cual existen soluciones enteras.

Hagamos cuatro filas de números (esquema 1). En la primera van los números naturales 1,2,…; en la segunda sus cuadrados 1, 4, 9, …; en la tercera la diferencia entre los cuadrados vecinos 3, 5, 7, …; en la cuarta las diferencias de las diferencias 2, 2, …

Los elementos de la segunda fila se obtienen sumando al cuadrado la diferencia, que es la serie de números impares, y se obtiene el cuadrado siguiente. Si nos fijamos en el número 25=(5)² vemos que se tiene:

144 + 25 = 169 (12)2 + (5)2 = (13)2

Es fácil generalizar esta fórmula obteniéndose:

que da una serie de soluciones enteras a la ecuación (2). La obtención de soluciones enteras en forma matemática y experimental puede hacerse con un computador.

En la serie de cuadrados 4, 9, …, se busca para uno cualquiera de los cuadrados si el menor tiene alguno que sumado al primero da el cuadrado elegido. Por ejemplo, para (5)² = 25, tenemos:

1 + 4 = 5	4 + 9 = 13	9 + 16 = 25
1 + 9 = 10	4 + 16 = 20	9 + 25 = 34
1 + 16 = 17	4 + 25 = 29
1 + 25 = 26

Teorema de Fermat

El teorema fue conjeturado  por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 por Andrew Wiles ayudado por Richard Taylor. La búsqueda de una demostración estimuló el desarrollo de la teoría algebraica de números en el siglo XIX y la demostración del teorema de la modularidad en el siglo XX.

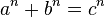
Si n es un número entero mayor que 2, entonces no existen números enteros a, b y c, tales que se cumpla la igualdad (con a,b,c no nulos):

El teorema fue conjeturado por Pierre de Fermat en 1637, pero no fue demostrado hasta 1995 por Andrew Wiles ayudado por Richard Taylor